Pratiques compositionnelles

La pratique compositionnelle de Xenakis est très diversifiée : du calcul le plus complexe (théorie des groupes ou formules probabilistes) au graphique (glissandi) ; de préoccupations spatiales à des recherches sur des échelles de hauteurs. Je me limiterai ici à présenter brièvement un certain nombre de pratiques que l’on peut regrouper autour de trois catégories : morphogenèse, probabilités et expressions logiques.

- Morphogenèse

Un outil très important pour Xenakis fut le graphique sur du papier millimétré (avec, comme deux dimensions, la hauteur et le temps), qu’il traduisait ensuite en notation solfégique. C’est par cette méthode qu’il composa les sonorités totalement inouïes du début et de la fin de Metastaseis (1953-54), constituées de gigantesques champs de glissandi. Dans la section finale (Fig.2), les cordes, totalement individuées, partent d’un cluster étalé sur tout le registre et finissent par converger vers un unisson en suivant des lignes brisées —ce sont des glissandi linéaires.

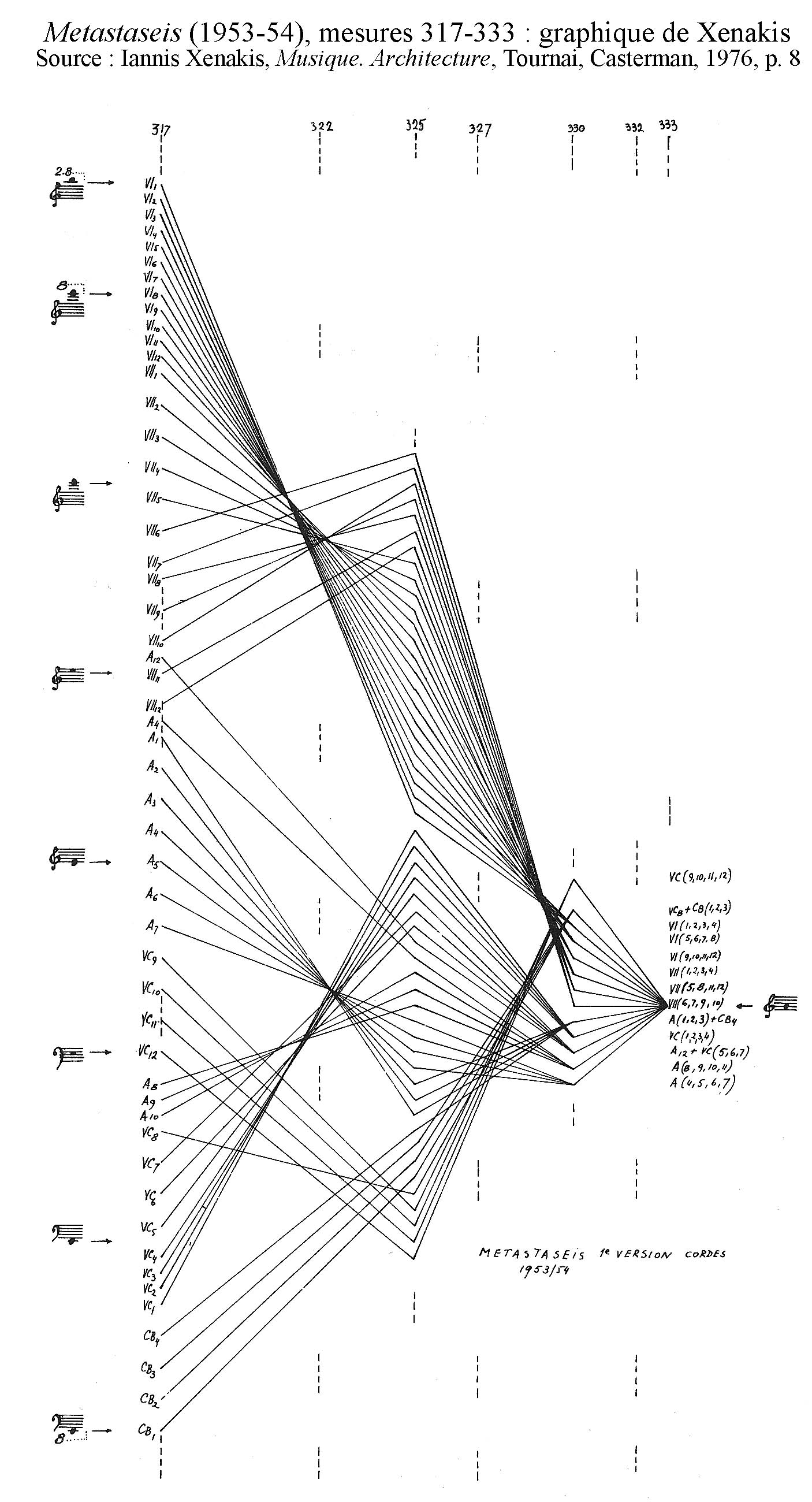
Fig.2 : Metastaseis (1953-54), mesures 317-333 : graphique de Xenakis Source : Iannis Xenakis, Musique. Architecture, Tournai, Casterman, 1976, p. 8

D’autres exemples de formes plastiques sont fournis par les « mouvements browniens » lorsque, dans les années 1970, Xenakis les transfère à la musique instrumentale : les courbes continues du graphique donnent des glissandi non-linéaires. Autre exemple : les arborescences.

Fig. 8 : Erikhthon (1974), arborescences : graphique de Xenakis Source : Iannis Xenakis, Musique. Architecture, Tournai, Casterman, 1976, p. 178

Il était normal que cette recherche aboutisse à l’invention de l’UPIC, où Xenakis dessine directement la courbe de pression du son ainsi que, à un second niveau, le développement du son dans le macrotemps.

Xenakis a peu parlé de ses graphiques, sinon en disant, à propos des mesures 52-59 de Pithoprakta (Fig.3), qu’ils constituent une « modulation plastique de la matière sonore » (Musiques formelles, p. 30). Avec le recul, il serait possible d’évoquer, à leur propos, des préoccupations morphogénétiques, et de les mettre en rapport avec sa quête d’une « morphologie générale ».

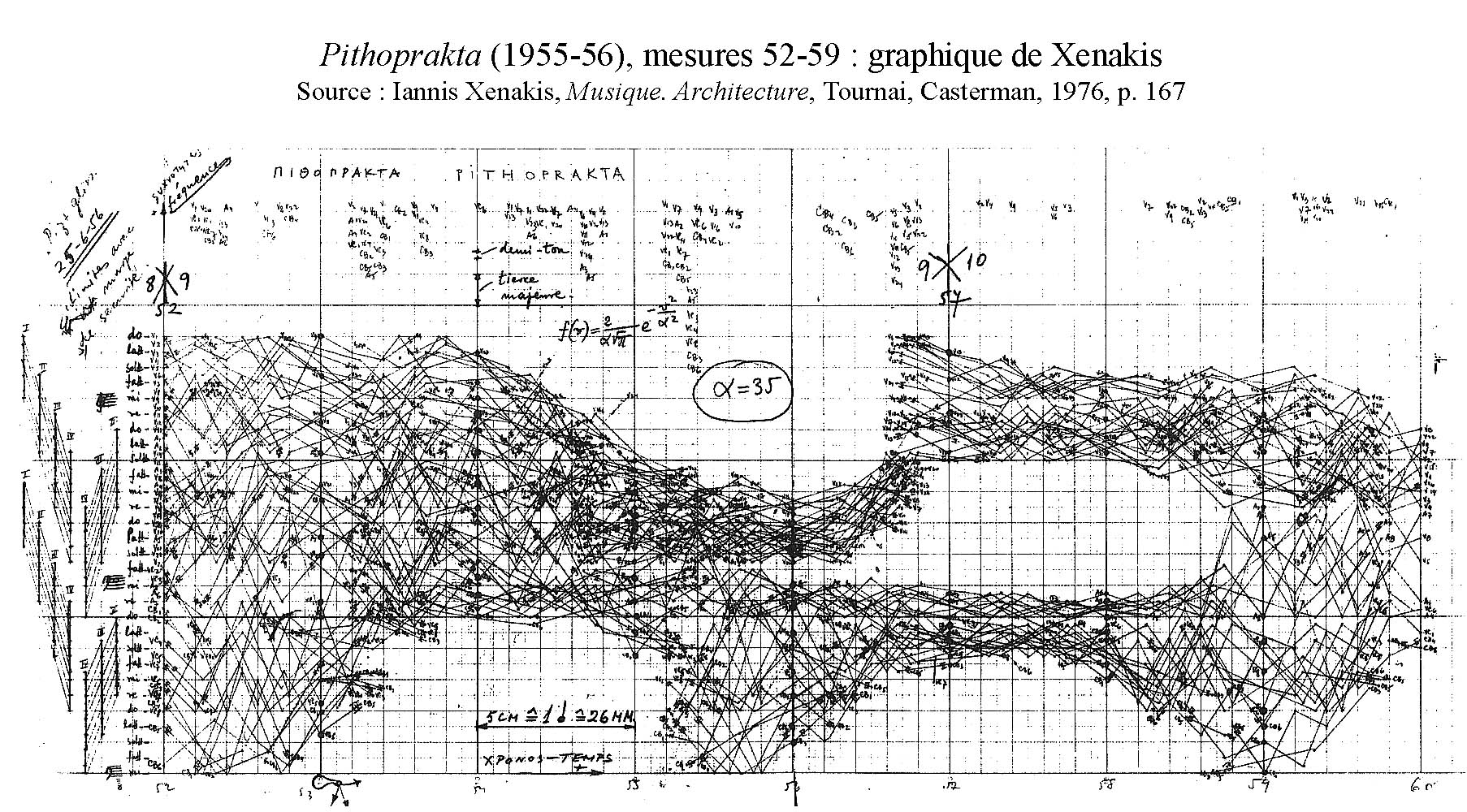
Fig.3 : Pithoprakta (1955-56), mesures 52-59 : graphique de Xenakis Source : Iannis Xenakis, Musique. Architecture, Tournai, Casterman, 1976, p. 167

Les analystes de la musique de Xenakis se servent fréquemment de transcriptions graphiques.

Fig.4 : Pithoprakta (1955-56), mesures 208-237 : transcription graphique (M. Solomos)

- Probabilités

Xenakis s’est servi des probabilités à plusieurs moments de son itinéraire musical et dans des buts différents. La révolution de Pithoprakta (le titre signifie « actions dues aux probabilités ») a été leur introduction pour calculer la distribution de sons formant un « nuage sonore ». Pour fonder sa démarche, Xenakis effectua une métaphore géniale : « Identifions les sons ponctuels, par exemple : pizz., aux molécules ; nous obtenons une transformation du domaine physique au domaine sonore. Le mouvement individuel des sons ne compte plus. L’effet massal et son évolution prennent tout un sens nouveau, le seul valable, lorsque les sons ponctuels sont en nombre élevé » (article de 1958, « Les trois paraboles », repris dans Musique. Architecture, p. 19). Ce transfert (de la physique moléculaire à la composition instrumentale) lui permit de réaliser les masses sonores qu’il reprochait aux sériels de donner à entendre, mais sans les composer directement. Rapidement, la question des probabilités, avec Achorripsis (1956-57), rejoint les préoccupations en matière de formalisation : Xenakis recherche le « minimum de contraintes » (cf. Musiques formelles p. 33-36) pour composer une œuvre musicale. Presque au même moment, avec la partie électroacoustique d’Analogique (1958-59), la vision probabiliste, appliquée cette fois au domaine du microson, préfigure la synthèse granulaire. En somme, Xenakis, dès ses débuts, explore trois philosophies des probabilités : le comportement de masses sonores ; l’idée d’une composition ex nihilo ; une vision granulaire du son.

A la fin des années 1960, il crée une synthèse sonore stochastique (probabiliste). Critiquant l’analyse de Fourier, il propose de dessiner directement la courbe de pression du son et, pour obtenir des sons riches, de générer ces courbes avec des fonctions probabilistes : des marches aléatoires ou « mouvements browniens ». A la fin des années 1980, avec le programme GENDY, il génère en continu du son à base de fonctions probabilistes (Gendy3, 1991).

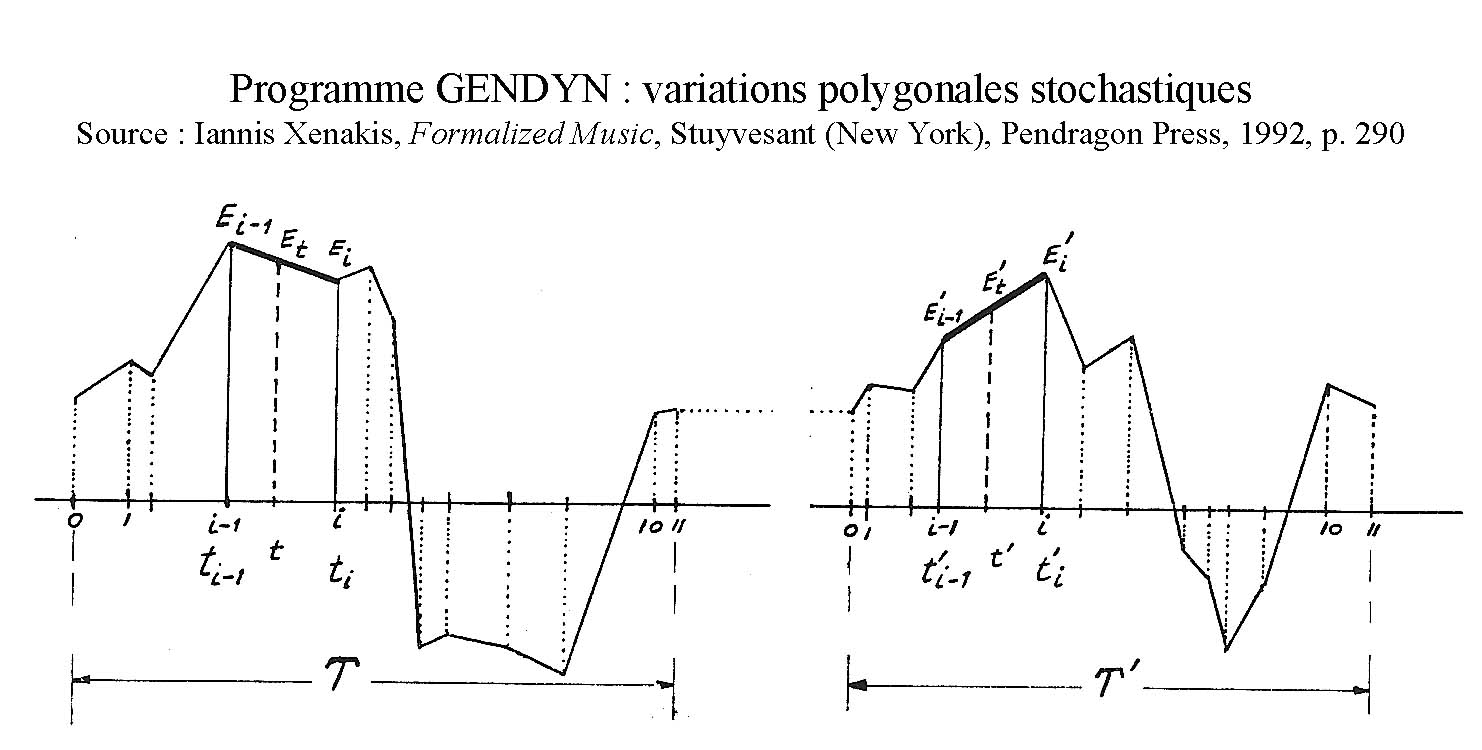
Fig.11 : Programme GENDYN : variations polygonales stochastiques Source : Iannis Xenakis, Formalized Music, Stuyvesant (New York), Pendragon Press, 1992, p. 290

- Expressions logiques

Le formalisme mathématique a intéressé Xenakis durant l’époque de Musiques formelles, avec la théorie des jeux (Duel, 1959), la théorie des ensembles (Herma, 1961) et la théorie des groupes (Nomos alpha, 1965-66, dont une partie de la formalisation est issue d’un groupe formé des rotations d’un cube .

Fig.6 : Nomos alpha (1965-66) : groupe des rotations du cube Source : Iannis Xenakis, Musique. Architecture, Tournai, Casterman, 1976, p. 98

De cette dernière découle une théorie qui lui est propre et que l’on retrouve dans plusieurs de ses œuvres : la théorie des « cribles ». Il s’agit d’un outil permettant de générer des échelles (qui peuvent être non octaviantes, utiliser des micro-intervalles, etc.). L’expression logique d’un crible utilise les opérations de la conjonction, de la disjonction et de la négation ainsi que la théorie des congruences : dans le total des valeurs possibles (par exemple, le total chromatique), un crible permet de choisir certaines valeurs (cf. Musique. Architecture, p. 38-70 et Kéleütha, p. 75-87). Xenakis utilise les cribles de hauteurs dans quelques pièces des années 1960, et il la généralise à partir de la fin des années 1970. Par ailleurs, certaines pièces de la fin des années 1960 et du début des années 1970 utilisent aussi des cribles de durées (Persephassa, 1969).

On pourrait appréhender également comme le résultat de l’application d’un formalisme mathématique les quelques sections d’œuvre que Xenakis compose, dans les années 1980, avec la théorie des automates cellulaires (Horos, 1986).